Abschnittsübersicht

  • Einklappen Ausklappen

    Allgemeines

    Alles einklappen Alles aufklappen

    • Herzlich Willkommen im Grundkurs Informatik 11 C2 zum Thema "Sicherer Kommunikation"!

      Nachdem im vorherigen Kurs Rechnernetze analysiert und Protokolle veranschaulicht wurden, wollen wir uns nun dem Aspekt der Sicherheit für unsere Kommunikation widmen. Dazu wollen wir verschiedene kryptografische Verfahren untersuchen und prüfen, ob diese den Kriterien an eine sichere Kommunikation genügen. 

      Hinweis: Stand 2025-06-03 - Dieser Kurs wird aktuell gepflegt.

    • Kommunikation im Kurssystem

      Neben der direkten Kommunikation mithilfe des Moodle-Mitteilungsdienstes, der auch auf der App funktioniert, und der E-Mail-Option, gibt es öffentliche Austausch- und Informationsmöglichkeiten in den Foren.

    • Ankündigungen Forum

    • Software im Themenfeld

      Der Großteil der im Unterricht eingesetzten Programmwerkzeuge ist als Open Source oder Freeware deklariert. Für Hausaufgaben oder zum Nachvollziehen der Unterrichtsbeispiele kann der IoStick für die Sekundarstufe II benutzt werden. 

    • Software: Informatik on Stick (1 GB) Link/URL
    • CrypTool: Simulationen für kryptografische Verfahren Link/URL
  • Einklappen Ausklappen

    Sichere Kommunikation

    • Alle bisher untersuchten Kommunikationsprotokolle konnten wir entweder im Protokollmitschnitt oder auf dem Server mitlesen. Oftmals ist es jedoch nicht erwünscht, dass E-Mails- oder Web-Anfragen so einfach mitzuschneiden sind. Kritisch wird es insbesondere, wenn sensible Daten (Kennwörter, Benutzernamen, Finanzdaten, ...)  übermittelt werden müssen. 

    • Beispiel 1: Eingabe von Daten auf einer Website

      Natürlich erwartet der Nutzer, dass seine Daten nicht durch Dritte mitgelesen werden können. Leider zeigt sowohl der Browser als auch der Mitschnitt, dass dies nicht der Fall ist. Eine Verschlüsselung der Daten hätte die Vertraulichkeit hergestellt.

    • Beispiel 2: Empfang einer E-Mail

      Vielleicht haben wir ja die E-Mail erwartet, aber ist die auch "echt", also stammt sie tatsächlich von Berta? Doch es gibt noch ein Problem: vielleicht ist die Mail ja von Berta, doch könnten die Daten manipuliert/geändert worden sein. Ein Anruf könnte ergeben, dass Berta das Senden der E-Mail sogar abstreitet. Wenn sie aber eine Mail gesendet hat, denn darf es keine Möglichkeit geben, dass sie das bestreiten kann.

      Es ist also sehr sinnvoll, Datenintegrität, Authentizität und Verbindlichkeit sicherzustellen.

    • Sicherheitsziele

      In der Sekundarstufe I haben wir uns bereits mit der Verschlüsselung von Nachrichten als Maßnahme zur Herstellung der Vertraulichkeit intensiv beschäftigt (Stichworte Caesarscheibe und Vigenere-Quadrat). Einige kryptografische Verfahren mussten wir damals als unsicher einstufen. Nun ist es aber an der Zeit, auf alle Sicherheitsmerkmale zu achten. Außerdem benötigen wir noch ein Kriterium (außer der "Nichtbrechen"), das für gute kryptografische Verfahren spricht.

    • Das Prinzip von Kerckhoffs Aufgabe

    • Auguste Kerckhoffs (1883): 
      Das Verfahren muss im Wesentlichen unentzifferbar sein und darf keine Geheimhaltung erfordern.
      Die Schlüssel bedürfen weiterhin der Geheimhaltung.

      Bildquelle: Eugen Drezen, Historio de la Mondo Lingvo (Leipzig, 1931), 102

      • Es ist schwieriger, ein kompromittiertes Verfahren zu ersetzen als einen kompromittierten Schlüssel.
      • Es ist möglich, ein geheimes Verfahren durch Reverse Engineering zu rekonstruieren.
      • Es ist leichter, Fehler/Hintertüren im Verfahren zu entdecken, wenn dieses öffentlich untersucht wird.
      • Es ist leichter, in geheimen Verfahren Hintertüren zu verstecken.
    • Bewertung: Einsatz von Open Source Software Aufgabe

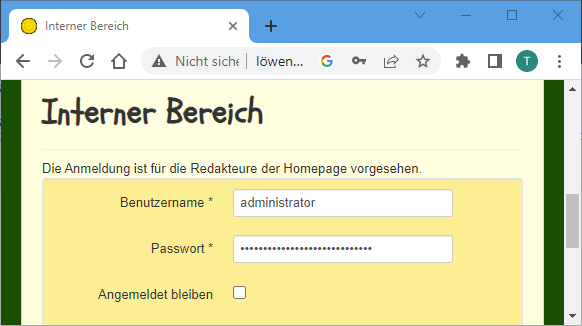
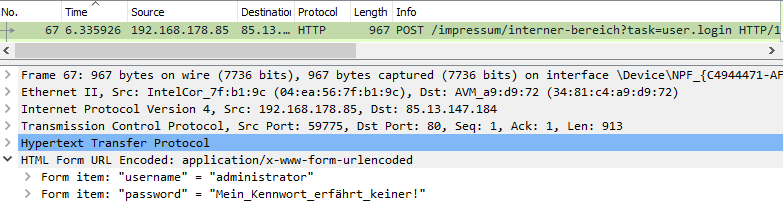
      Für die Realisierung der elektronischen Patientenakte wurden von den Krankenkassen Ausschreibungen für die Entwicklung der Software vorgenommen. Beurteilen Sie den nachfolgenden Auszug aus einer Ausschreibung.

  • Einklappen Ausklappen

    Historische mono- und polyalphabetische Verfahren

    • Dem Sicherheitsziel Vertraulichkeit haben wir uns schon in der Sekundarstufe I gewidmet und verschiedene kryptografische Verfahren - also Algorithmen zum Ver- und Entschlüsseln von Nachrichten untersucht. Dabei mussten wir einige Verfahren als unsicher einstufen, da die erzeugten Geheimtexte auch ohne Kenntnis des Schlüssels zu brechen waren.

      Im Folgenden wollen wir unser Wissen und Können reaktivieren.

    • Inf-Schule: Krypto-Stationen Link/URL

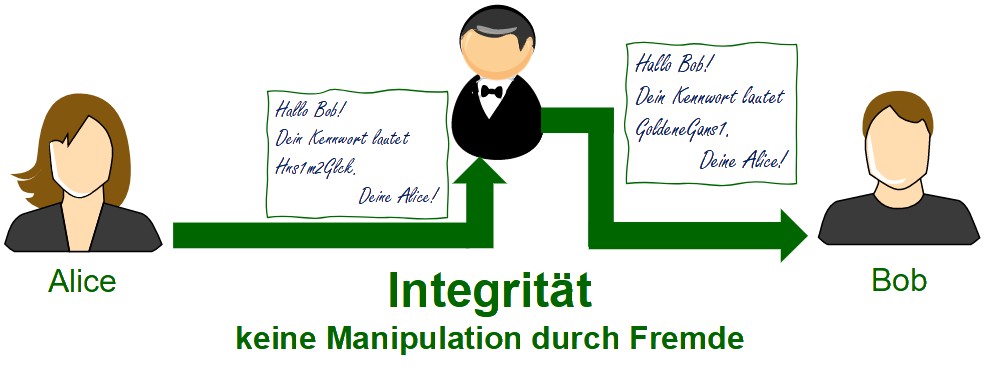
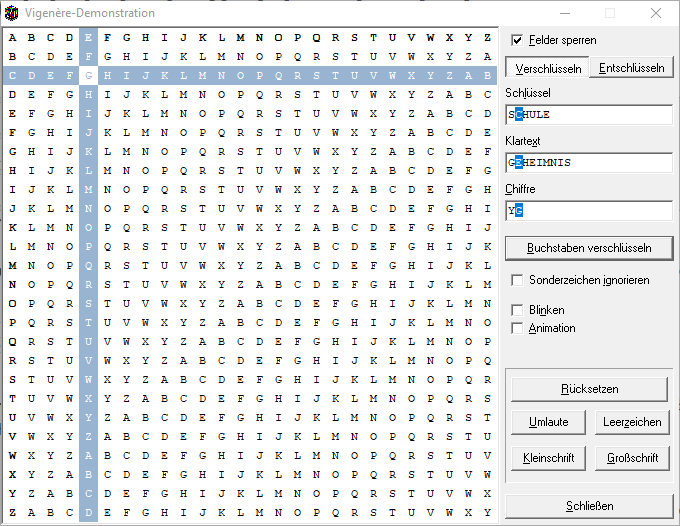
      Wiederholen Sie an den Stationen die Grundbegriffe und Grundprinzipien klassischer kryptografischer Verfahren. Realisieren Sie die Übungen zum Ver- und Entschlüsseln sowie zum Brechen der Verschlüsselung.

      Bewerten Sie die Verfahren jeweils hinsichtlich der Sicherheitsziele und des Prinzip von Kerckhoffs. 

    • Übungen zu historischen Verfahren Aufgabe
    • Cäsar-Scheibe Textseite
    • Datenverschlüsselung Externes Tool
      Nicht verfügbar, außer: Sie sind in einer Gruppe

    • Zusammenfassung

      Im Kontext der Verfahren haben wir die Begriffe Klartext, Geheimtext, Klartextalphabet, Geheimtextalphabet und Schlüssel wiederholt. Die Tätigkeiten sind verschlüsseln und entschlüsseln.

      Alle bisherigen Verfahren sind symmetrische Verfahren. Sie verwenden zum Ver- und Entschlüsseln den gleichen Schlüssel. 

      Monoalphabetische Verfahren verwenden genau ein Geheimtextalphabet. Beim Caesar-Verfahren ist dies beispielsweise das um mehrere Stellen verschobene Klartextalphabet. 

      Klartextalphabet

      A

      B

      C

      D

      E

      F

      G

      H

      I

      J

      K

      L

      M

      N

      O

      P

      Q

      R

      S

      T

      U

      V

      W

      X

      Y

      Z
      Geheimtextalphabet 

      D

      E

      F

      G

      H

      I

      J

      K

      L

      M

      N

      O

      P

      Q

      R

      S

      T

      U

      V

      W

      X

      Y

      Z

      A

      B

      C

      Polyalphabetische Verfahren verwenden mehrere Geheimtextalphabete. Beim Vigenère-Verfahren erfolgt die Auswahl des Alphabets anhand des jeweiligen Schlüsselbuchstabens.

      Alle bisher besprochenen Verfahren können nicht zur Herstellung des Sicherheitsziels Vertraulichkeit verwendet werden, da sich damit verschlüsselte Texte mithilfe von statistischen Methoden ohne Kenntnis des Schlüssel in den Klartext überführen lassen. Das Brechen der Verschlüsselung sollte jedoch unmöglich oder zumindest nur mit extrem hohen Ressourcenaufwand möglich sein.

      Nachweislich perfekte Sicherheit bietet das One-Time-Pad (OTP). Es basiert auf dem Vigènere-Verfahren und setzt zusätzlich folgende Bedingungen:

      1. Die Schlüssellänge ist gleich der Klartextlänge.
      2. Der Schlüssel besitzt eine zufällige Zeichenreihenfolge.
      3. Der Schlüssel wird nur einmalig verwendet.


      Das OTP erfüllt das Sicherheitsziel Vertraulichkeit und Kerckhoffs Prinzip      . Für alltägliche sichere Kommunikation ist es aber nicht nutzbar.

      Alle Verfahren haben das Problem, dass beide Kommunikationsparteien den gleichen Schlüssel besitzen müssen. Sollen alle Menschen auf der Welt miteinander verschlüsselt kommunizieren, dann muss ich mit jedem Menschen auf der Welt einen individuellen Schlüssel vereinbaren. Nutze ich einen Schlüssel mehrfach, so können mehrere Personen die Nachricht mitlesen.

      Versuchen wir nun, das Problem der Schlüssel zu lösen.

    • Übung OTP Aufgabe
    • Gemischte Übungen (aus Klasse 7) Verzeichnis
  • Einklappen Ausklappen

    Asymmetrischen kryptografische Verfahren und deren Anwendung zum Schlüsseltauschen, Signieren und Zertifizieren

    Hervorgehoben

    • Wir haben eine Schlüsselproblem! Unabhängig vom ausgewählten kryptografischen Verfahren müssen wir unserem Kommunikationspartner den gemeinsamen geheimen Schlüssel übermitteln.

      Gibt es eine Möglichkeit einen geheimen Schlüssel so zu übermitteln, dass wir keine geheimen Schlüssel vorher austauschen müssen?

      Versuchen wir es anschaulich: Unsere Kommunikationsteilnehmer Alice und Bob haben je ein Schloss mit Schlüssel. Alice möchte Bob ein Geheimnis in einer Kiste sicher übermitteln. Bob hat keinen Zugriff auf den Schlüssel von Alice und soll diesen auch niemals haben. Wie kann Alice agieren?

    • Clip: Sicher Kommunizieren - einfach erklärt Link/URL
    • Asymmetrische Verschlüsselung

    • Bei der asymmetrischen Verschlüsselung (Public-Key-Verfahren) besitzt jeder Kommunikationsteilnehmer zwei Schlüssel: einen öffentlichen Schlüssel, der allen Nutzern zur Verfügung gestellt wird und einen privaten Schlüssel, den nur der Nutzer besitzt. Zum Versenden einer Nachricht wird der Klartext mithilfe des öffentlichen Schlüssels dem Empfängers verschlüsselt. Der Empfänger kann dann mithilfe seines privaten Schlüssels die Nachricht entschlüsseln.

      Beide Schlüssel werden so berechnet, dass aus dem einen Teil der andere Teil nicht ermittelt werden kann. Die Regeln zur Schlüsselbestimmung und Anwendung sind komplexe mathematische Verfahren unter Benutzung zahlentheoretischer Sätze und großer Primzahlen. 

      Damit es keine komplizierte Mathematik gibt, nutzen wir den ASYM-Coder (in der Online-Version) aus dem Buch "Abenteuer Informatik" von Jens Gallenbacher und werden uns erst später mit etwas Mathematik beschäftigen.

    • ASYM-Kodierer aus Gallenbacher: Abenteuer Informatik Datei
    • Zwei Schlüssel? Aufgabe
    • AB Asymmetrisches Verfahren 1 Datei


    • Schlüsselberechnung und Einwegfunktion

      Die beiden Schlüssel werden mithilfe mathematischer Berechnungen aus großen natürlichen Zahlen erzeugt. Für das RSA-Verfahren, benannt nach den Entwicklern Ron Rivest, Adi Shamir und Leonard Adleman, lässt sich dies mit der Demo im Tool CrypTool1 anschaulich zeigen. Das genaue Verfahren ist für uns hier nicht relevant.

      RSA-Demo (nur für Freaks!)

      Aber warum kann man aus dem öffentlichen Schlüssel und beispielsweise dem Geheimtext nicht auf den privaten Schlüssel schließen? Das Geheimnis sind sog. Einwegfunktionen, also mathematische Funktionen, die in die man in eine Richtung sehr leicht/schnell ausrechnen kann, aber deren Umkehrfunktion de facto unmöglich zu bestimmen ist.

      Beispiele:

      • leicht: Ausdrücken der Zahnpastatube
        schwer: Hineinpressen der Zahnpasta in die Tube (insbesondere wenn es eine zweifarbige Zahnpasta war!)
      • leicht: Backen eines Kuchens
        schwer: das Zerlegen des Kuchens in seine Bestandteile (oder sogar das Bestimmen der Bestandteile)
      • leicht: Einwerfen eines Briefes in einen Postkasten
        schwer: Herausholen des Briefes (es sei denn, man hat den geheimen Schlüssel)
      • leicht: Mischen einer Farbe aus den Grundfarben eines Farbkastens
        schwer: Zerlegen einer Farbe in die Grundfarben eines Farbkastens
      • leicht: Rutschen von einer Rutsche
        schwer: Hinaufkletten auf der Rustche
      • leicht: Multiplizieren zweier natürlicher Zahlen
        schwer: Zerlegen eines Produkts in zwei Faktoren
    • Übung zu Einwegfunktionen Aufgabe
    • Nur für Freaks: RSA exemplarisch Textseite
    • Digitales Signieren – Hashfunktion
    • Digitale Signatur Externes Tool

    • Eine digitale Signatur (Unterschrift) sichert Verbindlichkeit und Authentizität des Absenders. Beide Ziele lassen sich durch asymmetrische Verschlüsselung erreichen.

      Zum Signieren einer Nachricht verschlüsselt der Erzeuger diese mit seinem geheimen Schlüssel. Er veröffentlicht Klartext und die erzeugte Signatur. Jeder Nutzer kann nun mithilfe den öffentlichen Schlüssels des Erzeugers zum Entschlüsseln der Signatur nutzen. Erhält er eine identische Kopie der Nachricht, dann war die Signatur echt.

      In der Realität ist es jedoch sehr ungünstig, das Klartextdokument und ein ebenso großes Dokument, welches die Unterschrift darstellt zu erzeugen und zu übermitteln. Daher signiert man nicht den Klartext, sondern die gehashter Form des Klartextes. 

      Das Anwenden einer Hash-Funktion auf einen Dokument erzeugt einen Hashwert, der folgende Eigenschaften besitzt:

      • Kompression: Nachrichten beliebiger Länge werden auf Nachrichten einer festen Länge komprimiert.
      • Einwegfunktion: Aus dem Komprimat kann man nicht auf die Nachricht schlussfolgern.
      • Kollisionsresistenz: Es ist praktisch unmöglich, zwei verschiedene Nachrichten mit dem gleichen Hashwert zu finden.

      Da eine Hash-Funktion beliebigen Text jeweils in einen Hash-Wert fester Größe umwandelt, muss es Texte mit gleichem Hash-Wert geben! Kollisionsresistenz bedeutet, dass es praktisch unmöglich ist, solche Kollisionen zu erzeugen.

      Für Freaks: Beispiel für MD5-Kollisionen (Tipp: beide Dateien in Cryptool hashen)

    • Inf-Schule: Experimente mit der (unsicheren) MD5-Hashfunktion Link/URL
    • MD5-Hasher Datei
    • Hashen, salzen, pfeffern - Kennwörter sicher speichern Link/URL
    • Zertifikate und Trust Center

    • Man-in-the-middle-Angriff Aufgabe

    • Das bisherige asymmetrische Verfahren hat einen großen Nachteil: die Übermittlung des öffentlichen Schlüssels kann manipuliert werden.

      Mithilfe von Zertifizierungsstellen, sog. Trust Center lässt sich dieses Problem lösen. Der öffentlichen Schlüssel des Trust Centers wird als Zertifikat im digitalen Endgerät gespeichert und beispielweise vom Betriebssystem regelmäßig überprüft. Trust Center verwalten ggf. auch die öffentlichen Schlüssel anderer Teilnehmer, die sich dafür persönlich im Trust Center vorstellen und authentifizieren müssen.

    • Inf-Schule: PKI Link/URL
    • Diffie-Hellman-Schlüsseltausch
    • Inf-Schule: Diffie-Hellman-Schlüsseltausch Link/URL

    • Für Freaks: Rechnet man mit Resten ist auch die diskrete Exponentialfunktion f(x) = sx mod p mit x ∈ ℕ relativ leicht ausführbar, während die diskrete Logarithmusfunktion aktuell praktisch unmöglich ist. 

      Beispiele (nach Beth, Thomas: "Sichere offene Datennetze". Im Dossier Kryptographie. Spektrum der Wissenschaft, 2001):

      1. Diskrete lineare Funktion f(x) = x + 42 mod 127
      2. Diskrete lineare Funktion f(x) = 7x + 63 mod 127
      3. Diskrete quadratische Funktion f(x) = (x - 63)2 + 42 mod 127
      4. Diskrete Exponentialfunktion f(x) = 3x + 63 mod 127

      Die diskrete Exponentialfunktion kann man nun nutzen, um beispielsweise für ein symmetrisches Verschlüsselungsverfahren einen gemeinsamen Schlüssel in aller Öffentlichkeit zu generieren. Entwickelt haben diesen Algorithmus 1976 die beiden Wissenschaftler Whitfield Diffie und Martin Hellman.

    • Mit dem Diffie-Hellmann-Schlüsseltausch wird die Brücke zur symmetrischen Verschlüsselung gebaut und ein sicherer Schlüsselaustausch möglich.

      • Moderne symmetrische Verschlüsselungsverfahren (AES, TwoFish, Tripple-DES, RC5) arbeiten sehr effizient. Das Problem ist der Austausch des geheimen Schlüssels.
      • Asymmetrische Verschlüsselungsverfahren sind langsam und aufwendig. Die Sicherheit steckt in der Verwendung von getrennten Schlüssel (privat/öffentlich), da kein Schlüsseltausch notwendig ist.

      Hybride Verfahren führen beide Vorteile zusammen: Um eine sichere Kommunikation zwischen zwei Partnern zu realisieren (beispielsweise via TCP), könnte zunächst der Diffie-Hellmann-Schlüsseltausch zum Erzeugen eines zufälligen langen geheimen Schlüssels auf beiden Seiten genutzt werden. Anschließend wird mithilfe des erzeugten Schlüssels die Nachricht symmetrisch verschlüsselt, übertragen und entschlüsselt. Wird eine neue Verbindung aufgebaut, erfolgt ein neuer Schlüsseltausch. Dadurch werden stets neue Schlüssel erzeugt und ein Einbruch in die digitale Kommunikation erschwert. 

      Ein Darstellung der hybriden HTTPS-Verschlüsselung findet sich unter inf-schule.de.

  • Einklappen Ausklappen

    Zusammenfassung

  • Einklappen Ausklappen

    Informatiker

    • Würdigung von Informatikern oder informatischen Errungenschaften Aufgabe
      Geöffnet: Sonntag, 1. Juni 2025, 00:00
      Fällig: Montag, 30. Juni 2025, 23:59

      Erstelle ein Poster zur Würdigung der Verdienste einer Person(engruppe), eines revolutionären Systems oder eines fundamentalen Konzepts/Algorithmus aus dem Bereich der Informatik nach dem Vorbild der GI-Poster.

      Beispiele:

      • Personen: John Presper Eckert und John William Mauchly, Ray Tomlinson, Karl Steinbuch, Claude Shannon, Herman Hollerith, Edgar F. Codd und Peter Chen, Clifford Berry und John Atanasoff, Stephen Wozniak, Niklaus Wirth, Richard Stallman, Marvin Lee Minsky, Claude Shannon, John McCarthy, J. C. R. Licklider, Alan Kay, David A. Huffman, Maurice V. Wilkes, Ronald L. Rivest, Adi Shamir, Leonard Adleman, Vinton G. Cerf und Robert E. Kahn, Whitfield Diffie und Martin E. Hellman, ...
      • Systeme: Zuse Z3, Apple 1, Difference Engine, Altair 8080, ...
      • Konzept/Algorithmus: Wegsuche, Quicksort, ER-Modell, Moore/Mealy-Automat, ...

      Die Bilder sollten einer CC-Lizenz genügen, statt des GI-Logos ist das Logo der Schule zu verwenden. Alle Bilder müssen auch auf A1/A2-Ausdrucken "gut" aussehen (hohe Auflösung). Die Einteilung/Zuordnung nehmen wir vor. Die Abgabe erfolgt als PDF- und Datei/Canva-Freigabe-Link.

      Termin der Abgabe: 30.06.2025

      Nicht verfügbar, außer: Sie sind in LK_11
    • Posterwahl Abstimmung
      Geöffnet: Freitag, 20. Juni 2025, 09:00
      Geschlossen: Dienstag, 24. Juni 2025, 23:00
      Nicht verfügbar, außer: Sie sind in LK_11