Akzeptor und Sprache

Endliche Automaten ohne Ausgabe - Akzeptor

Ein Safe öffnet sich nur dann, wenn die vierstellige Ziffernkombination korrekt eingegeben wurde. Eine Smartphone lässt sich nur dann bedienen, wenn eine PIN oder der Fingerabdruck korrekt sind. Beide Fälle lassen sich durch einen Automaten beschreiben. Eine Ausgabe nach jedem Schritt ist jedoch nicht mehr erforderlich. Erst am Ende der Eingabe muss entschieden werden, ob diese akzeptiert oder nicht akzeptiert wird. Solche Automaten nennt man Akzeptoren.

Definition des Akzeptors - Automat ohne Ausgabe

Ein Akzeptor A = (X, Z, δ, z₀, Z_E) ist ein endlicher Automat ohne Ausgabe. Dabei gilt:

• • X ... Eingabealphabet (nichtleere, endliche Menge)
  • Z ... Zustandsmenge (nichtleere, endliche Menge)
  • δ ... Überführungsfunktion, welche jedem Paar (Eingabezeichen, Zustand) genau einen Folgezustand zuordnet
  • z₀ ∈ Z ist der Anfangszustand
  • Z_E ... Endzustandsmenge (nichtleere, endliche Teilmenge von Z)

Aufbau eines Funktionsmodells

Arbeitsweise

• SOLANGE sich in der Zelle des Lesekopfs ein Zeichen befindet:
  • Lies mithilfe des Lesekopfs das Zeichen aus der aktuellen Zelle des Eingabeband
  • Wechsle in Abhängigkeit vom aktuellen Zustand und dem gelesenen Zeichen in einen Folgezustand.
  • Bewege das Band eine Zelle weiter.
• Falls der aktuelle Zustand ein Endzustand ist, dann aktiviere die Akzeptanzanzeige.

Wörter und Sprache

• Ein Wort w ist eine Kombination von Zeichen aus einem Alphabet X.
• Die Menge aller Wörter über einem Alphabet X ist unendlich groß.
  Beispiel: Wenn X = {a, b}, dann ist die Menge aller Wörter X* = {ε, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, bbb, aaaa, aaab, ...}.
• Die Sprache eines Automaten L(A) ist die Menge aller Wörter über dem Alphabet X, die A in einen Endzustand überführen. 
• Die Sprache kann verbal, durch die Angabe eines Musters, mathematisch oder durch Auflisten aller Wörter beschrieben werden, beispielsweise so:
  L(A) = {00, 000, 100, 0000, 0100, 1000, 1100, …} 
  L(A) ist die Menge alle Binärzahlen, deren letzten beiden Bits Null sind. 
  L(A) ist die Menge aller durch 4 teilbaren Binärzahlen.
  L(A) = {w | w ∈ X* und w endet auf 00}

Beispiel: Safe mit vierstelligem Ziffernschloss

Ein elektronischer Safe lässt sich nur dann öffnen, wenn die Ziffernkombination 0815 eingegeben wird. Alle anderen Eingaben sperren den Safe dauerhaft.

Dies lässt sich als Akzeptor A = (X, Z, δ, q₀, Z_E) modellieren mit

• • X = {0, 1, ..., 9}
  • Z = {q₀, q₁, q₂, q₃, q_4, q₅}
  • δ als Tabelle
    
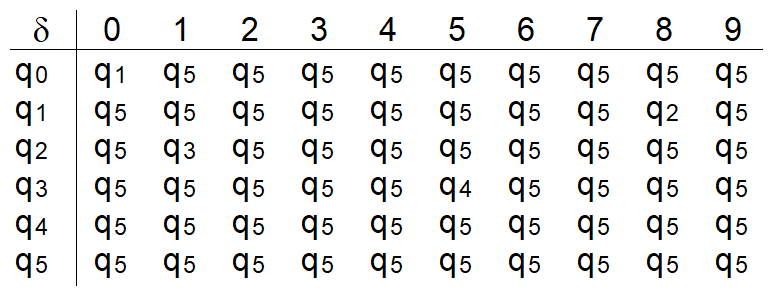
    oder als Graph
    
  • q₀
  • Z_E = {q₄}

Die Sprache L(A) des Automaten besteht einzig aus dem Wort w = 0815, L(A) = {0815}.