Informatik 11 GK/LK: B Konzepte der theoretischen und technischen Informatik - Herr Hempel
Abschnittsübersicht
-
-
-
Der Mealy-Automat MA = (X, Y, Z, δ , λ , q0) simuliert ein Verschlüsselungsverfahren, das nur mit Ziffern als Eingabezeichen arbeitet. Die Abbildung zeigt den Graph der Überführungsfunktion.

- Geben Sie die Mengen X, Y und Z an.
- Verschlüsseln Sie die Zahlenfolge 0 - 8 - 1 - 5 und entschlüsseln Sie die Nachricht 18 - 24 - 12 - 14.
- Entwickeln Sie einen Automaten mit Ausgabe, der nach diesem Prinzip verschlüsselte Nachrichten entschlüsselt. Der Automat soll dabei die Eingabe ziffernweise entgegen nehmen, also für obiges Beispiel statt 18 - 24 - 12 - 14 die Form 1 - 8 - 2 - 4 - ...
-
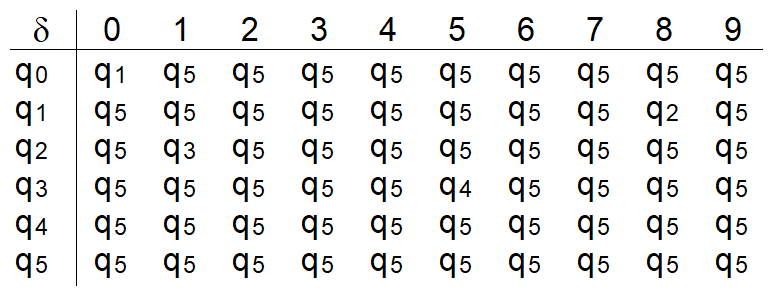
Lösung zur Aufgabe "Primitiver Verschlüsselungsautomat" Textseite
-
-
Lösungen zu den Aufgaben aus der Zusammenfassung "Akzeptor und Sprache" Textseite
-
Lösungen Akzeptor in Anwendungen Textseite
-
Lösungen Akzeptor mit ab- bzw. 01-Sprachen Textseite
-
-
Informationen über das Leben und Wirken von Alan Turing (ab Minute 8:50) Externes Tool
-
Lösung zur Aufgabe S. 8 Textseite
-
Lösung der Übungsaufgaben zur TM Textseite
-
-
Lösungen Verzeichnis
-
Ein Programm (GK: Scratch, LK: Java/Python) sucht magische Quadrate von Typ 3x3 auf eine logische, aber nicht sehr effektive Art. Es probiert einfach alle Varianten aus.
- Schätze spontan die Zeit bis zur Ausgabe einer ersten Lösung für deinen Computer. Probiere erst dann das Programm aus.
- Beschreibe die prinzipielle Arbeitsweise des Programms.
- GK/Scratch:
- Füge den Baustein "zeige_Variablen" als 3. Block in das Ereignis "Wenn grüne Flagge angeklickt" ein und prüfe den Programmablauf.
- Füge an einer geeigneten Stelle des Programms den Block "zeige_Stoppuhr_und_warte" ein, um die Laufzeit bis zum vollständigen Durchlauf abzuschätzen.
- LK/Java/Python:
- Lasse Dir mithilfe der Systemzeit die Laufzeit für einen Block so ausgeben, dass du daraus auf die Laufzeit des gesamten Programms mathematisch schließen kannst.
- Schätze die Laufzeit eines gleichartigen Programms für 4x4-Quadrate.
-
Collatz Lösung Java Datei
-
-
-
Geschichte der Computer - Abschnitt: Die ersten Computer der Welt Externes Tool
-
Erarbeiten Sie unter Verwendung der Lehrbücher Informatik 2 Schöningh S. 234ff. und Oldenbourg S. 88ff. sowie des Arbeitsblattes den Aufbau und die acht Prinzipien der von-Neumann-Architektur.
-
01 AB von Neumann Lösung Datei
-
AB Johnny Lösungen Datei
-
Lösung 4_3a-c Datei
-
Eine Kritik am von-Neumann-Konzept wurde 1977 von Turing-Award-Preisträger John W. Backus geübt:
„Sicherlich muss es auf eine weniger primitive Art möglich sein, große Änderungen auf dem Speicher durchzuführen, als riesige Mengen von Datenwörtern vor und zurück durch den Von-Neumann-Flaschenhals zu schieben. Diese Röhre bildet nicht nur einen wörtlichen Flaschenhals für den Datenverkehr eines Problems [...], es ist ein intellektueller Flaschenhals, der uns an ein Denken „ein Datenwort auf einmal“ gebunden hat, anstatt uns zu ermutigen, in den Begriffen der größeren konzeptuellen Einheiten der vorliegenden Aufgabe zu denken.“
Ermitteln Sie mithilfe eines der bereits analysierten MOPS- oder Johnny-Programme, was mit dem Begriff "von-Neumann-Flaschenhals" gemeint ist. Recherchieren Sie Möglichkeiten, das Problem des Flaschenhalses zu reduzieren.
-
Einer der ersten Computer, der Mark I, wurde in Kooperation zwischen IBM und der Harvard-Universität entwickelt und 1944 in Betrieb genommen wurde. Er verwendete eine Rechnerarchitektur die sich von der von-Neumann-Architektur unterscheidet.
Ermitteln Sie mithilfe der angegebenen Website Gemeinsamkeiten und Unterschiede in der Architektur. Leiten Sie jeweils Vor- und Nachteile ab.
-
-
Lösungen Verzeichnis
-
Lösungen Verzeichnis

 Herzlich Willkommen im Kurs Informatik 11 B zum Thema "Konzepte der theoretischen und technischen Informatik"!
Herzlich Willkommen im Kurs Informatik 11 B zum Thema "Konzepte der theoretischen und technischen Informatik"!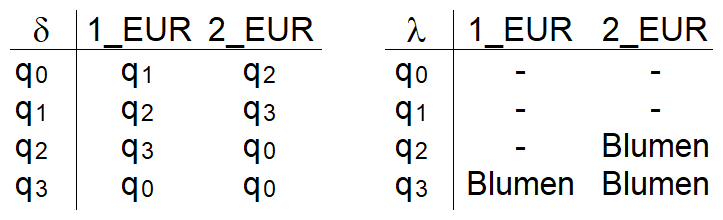






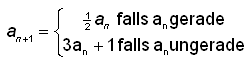
 Mit Akzeptor, Kellerautomat und
Mit Akzeptor, Kellerautomat und  Natürliche Sprachen ist die von Menschen gesprochene Sprache, die aus einer historischen Entwicklung entstanden ist. Künstliche Sprachen (Plansprache, Geheimsprache, ...) sind vom Menschen geschaffene Hilfssysteme und dienen der Codierung von Sprache z. B. für einen alternativen Übertragungsweg.
Natürliche Sprachen ist die von Menschen gesprochene Sprache, die aus einer historischen Entwicklung entstanden ist. Künstliche Sprachen (Plansprache, Geheimsprache, ...) sind vom Menschen geschaffene Hilfssysteme und dienen der Codierung von Sprache z. B. für einen alternativen Übertragungsweg. 
 Mit der
Mit der 

 Dass das Binärsystem für Rechenautomaten besonders günstig ist, erkannten Konrad Zuse (Deutschland) und George Stibitz (USA) in den 1930er Jahren. Die Mathematik dafür wurde von George Boole (USA) in der Mitte des 18. Jahrhunderts entwickelt.
Dass das Binärsystem für Rechenautomaten besonders günstig ist, erkannten Konrad Zuse (Deutschland) und George Stibitz (USA) in den 1930er Jahren. Die Mathematik dafür wurde von George Boole (USA) in der Mitte des 18. Jahrhunderts entwickelt.